Proportional ranked choice voting
Proportional ranked choice voting is the best model for proportional representation in the United States. It does not require a constitutional amendment but rather two statutory changes: a switch from single-winner districts to multi-winner districts and a new way to cast and count votes.
To elect more than one winner per election, states must stop electing candidates in single-winner districts and instead elect them statewide or, for states with six or more seats, in larger districts that each elect at least three winners.
To enable different groups to each win their fair share of seats, each voter must have one vote. That way, each winner represents a distinct group of participating voters. To avoid “wasted votes” that may undermine fair representation, voters must be able to rank their choices.
We can adopt proportional representation for the U.S. House of Representatives while retaining our tradition of voting for candidates rather than political parties; without changing the U.S. Constitution; and with voting rules that have been tested in local elections across the country. We can do this by adopting proportional ranked choice voting.
Proportional ranked choice voting would require two significant changes to U.S. House elections: A switch from single-winner to multi-winner districts and to ranked ballots and round-by-round counts to elect winners. Congress could compel all 50 states to make these changes tomorrow if it wanted to.
The new system would give voters more choice and a more expressive way to vote. All voters would experience competitive campaigns and would almost always elect at least someone they support. Currently, only two — and sometimes only one candidate — appear on the ballot, giving voters a paucity of choices. Further, most voters understand their vote has relatively little power because they know they live in safe Republican or Democratic districts.
These essential benefits are often lost because explanations about proportional ranked choice voting tend to focus on how votes are counted. Details about process are important, but voters must understand, first and foremost, that the system means more choices and more power, through the likelihood of having one’s vote actually work to elect a representative of one’s choice.
With that said, let’s dive into the process. One way to understand how the system works is to start with our goals. We want elections that result in proportional representation. What do we need to do to make that happen?
Multi-winner districts
First, to achieve proportional representation, contests must elect more than one person. Simply put, if one person wins, then only one group of voters — those who voted for the winner — have genuine representation. On the other hand, if two people win, then two groups of voters can win; no matter how much they disagree with each other, they can each elect their own representative. If three, four, or five win, then more of the spectrum can be represented, even if the voters continue to choose winners from the two major political parties.
For the U.S. House, that means states must stop dividing into single-winner districts. Instead, they must either elect candidates statewide or divide into larger districts that each elect multiple winners. The more seats elected, the more proportional the results.
The most proportional would be for all states to elect all members statewide, but that would come with tradeoffs. For one, the number of candidates would be huge in some states. If California elected all 52 of its House seats statewide, its ballot would have to include over 100 candidates. Electing all candidates statewide would also allow winners who represent as little as 2 percent of the statewide vote in some states, which would attract fringe candidates with extreme positions. That dynamic would play out only in the largest states, while the smallest states would elect five or fewer members. Larger states, in other words, would experience an entirely different political reality. For these reasons, proportional representation would work best for the United States if smaller states elect candidates statewide and larger states divide into regions that each elect at least three winners.
The term “district magnitude” refers to the number of winners in a particular district. Right now, we have districts of magnitude 1: Each district elects one winner. We want districts of at least magnitude 3 in states with at least that many representatives, because that is the smallest number that can ensure both minority representation and majority rule (the majority group can elect two of three seats while the minority group can elect the remaining one). For nearly a century, from 1870 to 1980, Illinois used a semi-proportional system called cumulative voting to elect its state house, and every district elected exactly three candidates, and sure enough, nearly every district elected two from the majority party, and one from the minority party. Ireland and Malta use proportional ranked choice voting in (mostly) five-winner districts. The Australian Senate uses proportional ranked choice voting in six-winner elections. Cambridge, Massachusetts, elects nine city councilors citywide with proportional ranked choice voting. What magnitude is ideal will depend on weighing different values.
The Fair Representation Act, a bill that would implement proportional ranked choice voting in U.S. House elections, would establish a maximum of five winners per district. Like the Irish model, it prioritizes five-winner districts followed by three-winner districts. Figure 7 shows what Wisconsin, North Carolina, and Tennessee might look like if divided into multi-winner districts per the Fair Representation Act.
Sample Fair Representation Act district maps


If the size of these districts gives you pause, keep in mind that candidates compete for their own constituencies within each district, and the number of votes needed to win a seat is relatively stable regardless of district size.
Figure 8 shows the number of votes needed to win in three scenarios: a single-winner district with 100,000 total votes cast; a three-winner district with 300,000 total votes cast; and a five-winner district with 500,000 total votes cast. As shown, the total number of votes needed to win a seat increases modestly as the size of the district grows.
Unless the constitution is amended, any proposal for proportional representation in the U.S. will have to include some states with magnitudes of only 1 or 2. Today, six states elect only one winner and seven states elect only two.[1] With so few seats elected, no system can really be called “proportional representation.”[2] As long as states vary greatly by population, and as long as the U.S. House stays a manageable size (say, fewer than 1,000 members), then there is no avoiding this.[3] These states should use ranked choice voting to improve voter choice and ensure a uniform ballot type across the country, but they unfortunately will not reap the benefits of proportional representation.
Multi-winner districts, on their own, are not a new idea. Some states used them to elect congressional representatives until 1970, and nine state legislatures continue to use them. However, most uses of multi-winner districts in the United States have not provided fair representation because they are winner-take-all. They treat every seat as a separate office, giving voters one vote per seat elected. Rather than providing representation to voters with different perspectives, this allows a single group to elect all winners and often results in partisan sweeps of the entire district. It has also served as a purposeful tool of racist oppression by denying representation to communities of color.
While multi-winner districts make it possible for distinct groups of voters to elect their own representatives, the voting method must ensure that the single largest group cannot win every seat. This is where ranked choice voting comes in.
Ranked choice voting
The simplest way to guarantee that different groups of voters can elect their own representatives is for every voter to cast only one vote in multi-winner districts — even though several candidates will win. If each voter has one vote, then each winner will necessarily have been elected by a distinct group of voters.
In fact, this approach — the single non-transferable vote system, also known as the single vote system — is in use in some places today. However, this method is only semi-proportional and has clear flaws. Imagine a race in which five winners will be elected and most voters choose to vote for the same, very popular candidate. As Figure 9 shows, that would mean that a minority of voters would be able to elect the other four winners, which would be wildly disproportionate.
Or, imagine if 15 candidates ran for five seats, and the vote splits nearly evenly among all of them. The five winners would collectively have only about a third of the votes cast; two-thirds of the votes would be spread out among the losing candidates and thus “wasted,” as Figure 10 shows.
Ranked choice voting effectively solves this problem. With proportional ranked choice voting, every voter has one vote, and the rankings ensure that as few votes as possible are wasted. Votes are counted round by round; in each round, any votes that would be wasted are counted for their next choices.
This method was invented in 1855 by Danish politician Carl Andræ and again (independently) four years later in England by political scientist Thomas Hare. Back then, voters ranked candidates in order of choice and put ballots into a box that was shaken up. Ballots were then removed one-by-one and sorted into piles based on their first choices.
If a candidate received enough votes to guarantee a win, then their pile was set aside; additional votes that ranked them first would instead go to the voters’ next choice. After all votes were counted, the candidate with the fewest votes was eliminated, and their ballots were added to their next choice. That repeated until eventually, the ballots were in roughly equal piles, one for each seat to be elected, each helping elect one candidate.
Since its beginning, it has worked. The method ensures that (1) the majority of voters elect a majority of the seats and (2) the minority also wins its fair share of seats. That two theorists independently devised it speaks to its efficacy. As an English officer said in 1862 when reporting on its use in Denmark:
I have heard [the system] called ridiculous and absurd, but after repeated inquiry I have been unable to discover why; and I have heard it called unintelligible, but it was by persons who had not tried to understand it; I have also heard it described as an impracticable law — an opinion which seems to me to be confuted by the fact that it has been in operation eight years, without any flaw having been brought to light in its machinery.[4]
The system has changed since then in two significant ways, both of which eliminate wasted votes. Both were posited by mathematicians and involve some mathematics to explain.
The election threshold
The phrase used above — “enough votes to guarantee a win” describes the election threshold. When the system was invented, the total votes were divided by the number of seats: To elect three candidates, each winner would receive one-third of the votes; put another way, winning one-third of the votes was therefore enough to be sure of winning one of the three seats.
Perhaps counterintuitively, candidates are guaranteed to win with fewer votes than that. Consider the election threshold to choose one winner. Requiring a candidate to earn 100 percent of the votes would be absurd. The actual threshold is a majority (greater than 50 percent of the votes). When one candidate reaches this threshold, a second candidate cannot possibly beat them. This logic also applies to multiple seats.
Suppose an election seeks three winners, and 100 votes are cast. A candidate with as few as 26 votes could not possibly come in fourth. Two other candidates might also get 26 votes each, but at that point, only 22 votes would remain (because 26 + 26 + 26 = 78, and 100 – 78 = 22). So, if a candidate in this scenario gets 26 votes, they will win.
Expressed generally, this lower election threshold equals the number of votes divided by the sum of one and the number of seats, plus one vote:
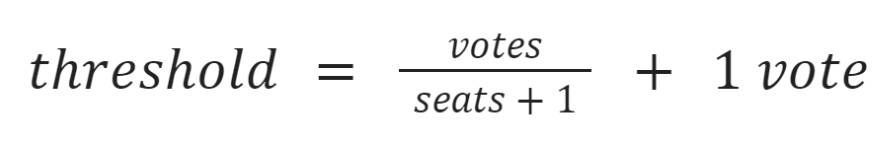
To elect three, a candidate must have 25 percent of the votes plus one; to elect four, a candidate must have 20 percent of the votes plus one, and so on. Table 3 shows the pattern up to five seats.
Identified by mathematician Henry Richmond Droop in 1869, this formula is sometimes called the “Droop quota.”
An important clarification: A smaller threshold does not indicate “less popular” candidates. A five-winner election should have five times as many voters as a single-winner election, so the absolute number of votes to win increases a little bit. Also, because multiple candidates win with their own equal shares of the vote, the total proportion of voters earning representation increases. With three winners, more than 75 percent of voters elect a candidate they support. With five winners, more than 83 percent of voters elect a candidate they support.
Each added seat gets us closer to full representation, with nearly every voter helping to elect someone they support. It also gets us closer to fair representation, because candidates elected proportionally represent distinct groups of voters. Further, this method incorporates the backup choices of those who are unable to elect their first choice.
Avoiding wasted votes
The other significant change to the system concerns extra or “surplus” votes. The old method deals with surplus votes by mixing up the ballots and then counting the first ones drawn for their top choice, and later ones for their next choice. Later developments replaced entirely random transfer by something more like a statistical sample. That approach works, and may still be the best approach in places with technical limitations, but it treats some ballots differently than others for apparently arbitrary reasons.
Australian mathematician J.B. Gregory came up with a different way of addressing surplus votes in 1880. He had an important insight: If the election threshold is 75 votes, and 100 ballots rank a particular candidate first, then the candidate has a surplus of 25 votes. We could randomly select 25 ballots to count for their next choices, or we could count three-fourths of each vote for its first choice, giving the candidate exactly 75 votes. The other quarter of each vote would count for its next choice, effectively transferring 25 votes total.
If this seems abstract, consider the possibility of 100 people with $1 each attempting to buy something that costs $75. They all put $1 toward the purchase and together are $25 over the price. We could give 25 of the people their dollar back, or we could give every person $0.25 back in change. Doing the latter does a better job of treating each person equally.
With Gregory’s method, no randomness is needed, and every vote is treated equally. The same number of votes transfer, but instead of a random sample, it is a perfectly proportional snapshot of all the next choices. Every voter still has exactly one vote, but some votes are divided among more than one candidate.
To find the proportion of each vote that will count for its next choice, divide the number of surplus votes the winning candidate earned by the total number of votes they earned.
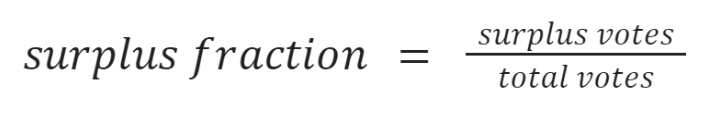
In the example above, the winning candidate had 100 votes, 25 more votes than needed, so 25/100 or 25 percent of each vote counts for its next choice.
Again, if this seems too abstract, imagine that each vote is worth $1, and the election threshold is the cost to win a seat. Voters give their full dollar to their first choice, and if their first choice winds up receiving more than they need to win, the voter gets some change back. The voter can then put their change toward their next choice; nothing is wasted. Applied to the political context, voters aren’t forced to “waste” their votes on popular candidates and are not “punished” for supporting them. It ensures that each person’s vote is as powerful as possible.
Counting round-by-round
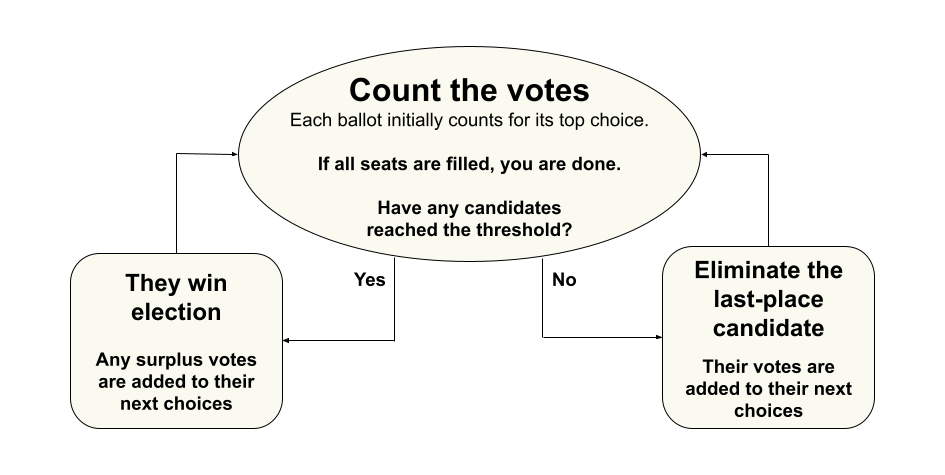
This list and the flow chart in Figure 12 summarize how votes are counted in a proportional ranked choice voting election:
Every vote counts for its top choice.
- If enough candidates have more votes than the threshold to fill every seat, then they win and the counting is complete; otherwise, proceed to the next step.
- Candidates who receive enough votes to clear the threshold are elected, and their surplus votes transfer to their voters’ next choices, with an equal fraction of each vote counting for its next choice; then repeat from step 2 above.
- If no active candidate (one that has not already been elected or eliminated in a prior round) is above the threshold, then the candidate in last place is eliminated, and all their votes transfer to their next choices; then repeat from step 2 above.
Proportional ranked choice voting tabulation flowchart
Because voters should not be forced to rank all candidates, every candidate ranked on a particular ballot might be either elected or eliminated. These “inactive” ballots are not included in later rounds, but the voter still has their say: Every candidate they expressed an opinion about (that is, ranked) either won or lost, and they abstain from future rounds.
This method was designed to ensure that, to the greatest extent possible, every vote cast contributes to the election of a candidate, and every voter has a representative who is at least somewhat accountable to them and who they helped elect. Every innovation to this method has improved on that goal, identifying and eliminating sources of wasted votes.
If this method seems complicated, keep these two points in mind: First, the voter has a very simple task — to rank the candidates in order of choice. This is a normal way of making decisions in everyday life; it’s not complicated. Think about it: When you go to buy breakfast cereal and find that your favorite is sold out, you can instead buy a second choice. When voters rank candidates, they almost always help elect someone they support — without needing to worry about how other people will vote when making their decisions.
Second, although the vote-counting involves multiple steps and some math, it is not arbitrary. Every step is laser-focused on making every vote as powerful as it can be. In this system, every voter has one vote and multiple candidates are elected. At its heart, it improves our democracy. Each step minimizes wasted votes and better guarantees full and fair representation.
The minimum proposal
What would a federal law look like that implemented proportional ranked choice voting in the U.S. House? How would Congress ensure that states elected members statewide in multi-winner districts and voters ranked choices that were tallied round-by-round?
Today, federal law requires that every state elect exclusively from single-winner districts. Congress should, at minimum, repeal this law. However, doing so without further action would be a step backward. This law was instituted to enhance civil rights by prohibiting states from using the “general ticket” statewide method, where voters cast one vote per seat elected. This method is winner-take-all on steroids, and it must not be permitted.
Congress could repeal the single-winner district mandate and outlaw the general ticket, giving states the option to adopt their preferred proportional or semi-proportional method. Some bills have been introduced to do just that.
But even a “bare minimum” proposal must go further. First, it should mandate multi-winner districts. Making them optional would do nothing if not exercised, and it’s unclear which states, if any, would exercise the option. The states most in need of reform – states like Texas or Illinois with the most severely gerrymandered districts – are the least likely to voluntarily adopt it. And states that might be willing to adopt the new system may not want to do so unilaterally: Any “blue” state adopting the system on its own would effectively make gerrymanders in “red” states even more powerful, and vice versa.
Second, the proposal should require proportional ranked choice voting and explicitly bar semi-proportional methods because they can seriously disrupt representation if too many voters vote for one candidate or if too many serious candidates participate.[5]
Putting these requirements together, a minimum proposal would:
- Require all states to use proportional ranked choice voting in general elections to the U.S. House.
- Require states that elect fewer than six representatives to elect all winners statewide.
- Allow states that elect six or more representatives to divide into districts, provided that each district has an equal number of people per representative elected and that no district elects fewer than three winners.
These ideas are not complicated. A bill incorporating them could fit on a single page.
Beyond the bare minimum
A law instituting this system could (and should) also include a number of other elements. The Fair Representation Act, which has been introduced over the past three cycles by Democratic Rep. Don Beyer of Virginia, meets minimum elements and also requires proportional ranked choice voting for primary elections, independent redistricting commissions for states that adopt district maps, and ranked choice voting for elections to the U.S. Senate, along with other elements.
The Fair Representation Act includes numerous good proposals. But even passing a “bare minimum” law would profoundly transform our system and our country. In Part 3, we will go through its many benefits.
Notes
[1] From smallest to largest, the single-winner states are Wyoming, Vermont, Alaska, North Dakota, South Dakota, and Delaware. The two-winner states are Montana, Rhode Island, Maine, New Hampshire, Hawaii, West Virginia, and Idaho.
[2] A single-winner election is always winner-take-all: One winner means one group of voters wins all representation in the district. With two winners, either the largest group wins both seats, or the majority group and the minority group equally split the district 1-1. Only with three or more winners can the majority group win a majority of seats while still allowing for minority representation.
[3] The U.S. House should add more members, as it regularly did prior to the 1929 Permanent Apportionment Act that fixed its size at 435 members. However, adding enough members to have no states with fewer than three representatives is not feasible: Using numbers from the U.S. Census taken in 2020, that would require the House to have 1,405 representatives.
[4] Salem Dutcher, Minority or Proportional Representation: Its Nature, Aims, History, Processes, and Practical Operation (1872). The English officer is listed only as “Mr. Lytton,” and described as an English secretary of legation at Copenhagen.
[5] Such a law could give states the option to use another fully proportional system, such as an open list system, but that would be an extra option beyond the bare minimum.
Contents
Part One:
The problems with
winner-take-all
Part Two:
Proportional ranked choice
voting explained
- Proportional representation in general
- Proportional ranked choice voting for the House